Tales de Mileto y Zenón de Elea

Tales de Mileto

Tales de Mileto fue un filósofo, matemático y astrónomo griego nacido alrededor del 624 a.C. en la ciudad de Mileto, en la región de Jonia (en la actual Turquía). Aunque poco se conoce con certeza sobre su vida, se le atribuyen numerosas contribuciones a la geometría y la filosofía, lo que lo convierte en uno de los primeros pensadores de la antigua Grecia.

Tales fue uno de los Siete Sabios de Grecia, una lista de filósofos y legisladores reconocidos por su sabiduría y contribuciones a la sociedad. Se cree que viajó extensamente por Egipto y Babilonia, donde pudo haber adquirido conocimientos matemáticos y astronómicos.

Entre sus aportes a la geometría se encuentran: 

Teorema de Tales: Se le atribuye la formulación del famoso teorema geométrico que lleva su nombre. Este teorema establece que si dos rectas paralelas son cortadas por una serie de líneas secantes, entonces los segmentos formados en una de las rectas son proporcionales a los segmentos correspondientes en la otra recta.

Medición de la altura de las pirámides: Se dice que Tales fue capaz de calcular la altura de las pirámides egipcias utilizando principios geométricos simples, como la semejanza de triángulos.

Predicción de eclipses: Tales fue uno de los primeros en predecir eclipses solares, demostrando su conocimiento avanzado en astronomía y geometría.

Su enfoque en la geometría y su habilidad para aplicarla a problemas prácticos sentaron las bases para el desarrollo posterior de esta disciplina.

Zenón de Elea

Zenón de Elea fue un filósofo griego nacido alrededor del 490 a.C. en la ciudad de Elea, en la Magna Grecia (en la actual Italia). Fue discípulo de Parménides, un influyente filósofo presocrático, y se le conoce principalmente por sus paradojas que desafiaron las nociones comunes sobre el movimiento y el infinito.

Zenón es famoso por sus contribuciones a la definición de continuidad e infinito en la filosofía y las matemáticas. Algunas de sus paradojas más conocidas incluyen:

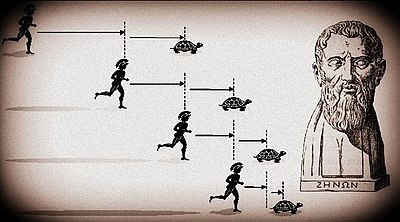
La paradoja de Aquiles y la tortuga: En esta paradoja, Zenón argumenta que Aquiles nunca podrá alcanzar a una tortuga en una carrera, ya que siempre tendrá que alcanzar el punto donde la tortuga estaba, pero para cuando llegue, la tortuga ya habrá avanzado un poco más.

La paradoja de la flecha: Zenón argumenta que el movimiento es imposible, ya que en cualquier instante de tiempo, la flecha parece estar en reposo, ocupando un punto en el espacio.

La paradoja del estadio: Esta paradoja se basa en la idea de que el espacio está compuesto por un número infinito de puntos, lo que lleva a conclusiones contradictorias sobre el movimiento.

Estas paradojas desafiaron las ideas tradicionales sobre el espacio, el tiempo y el movimiento, y tuvieron un profundo impacto en el desarrollo posterior de la filosofía y las matemáticas. Zenón fue uno de los primeros en explorar conceptos como el infinito y la continuidad, sentando las bases para la comprensión moderna de estas ideas.